Combinatorial optimisation with Gurobi
I used the mathematical programming solver Gurobi to find an optimal subset of climate models.
An important project in my PhD is the selection of a subset of climate models whose mean optimises a given cost function while respecting certain constraints. In my case, I am interested in minimising the root mean square error (RMSE) between an observational product (our “truth”) and the mean of a subset of climate models for a given subset size. This idea is illustrated in the figure below:
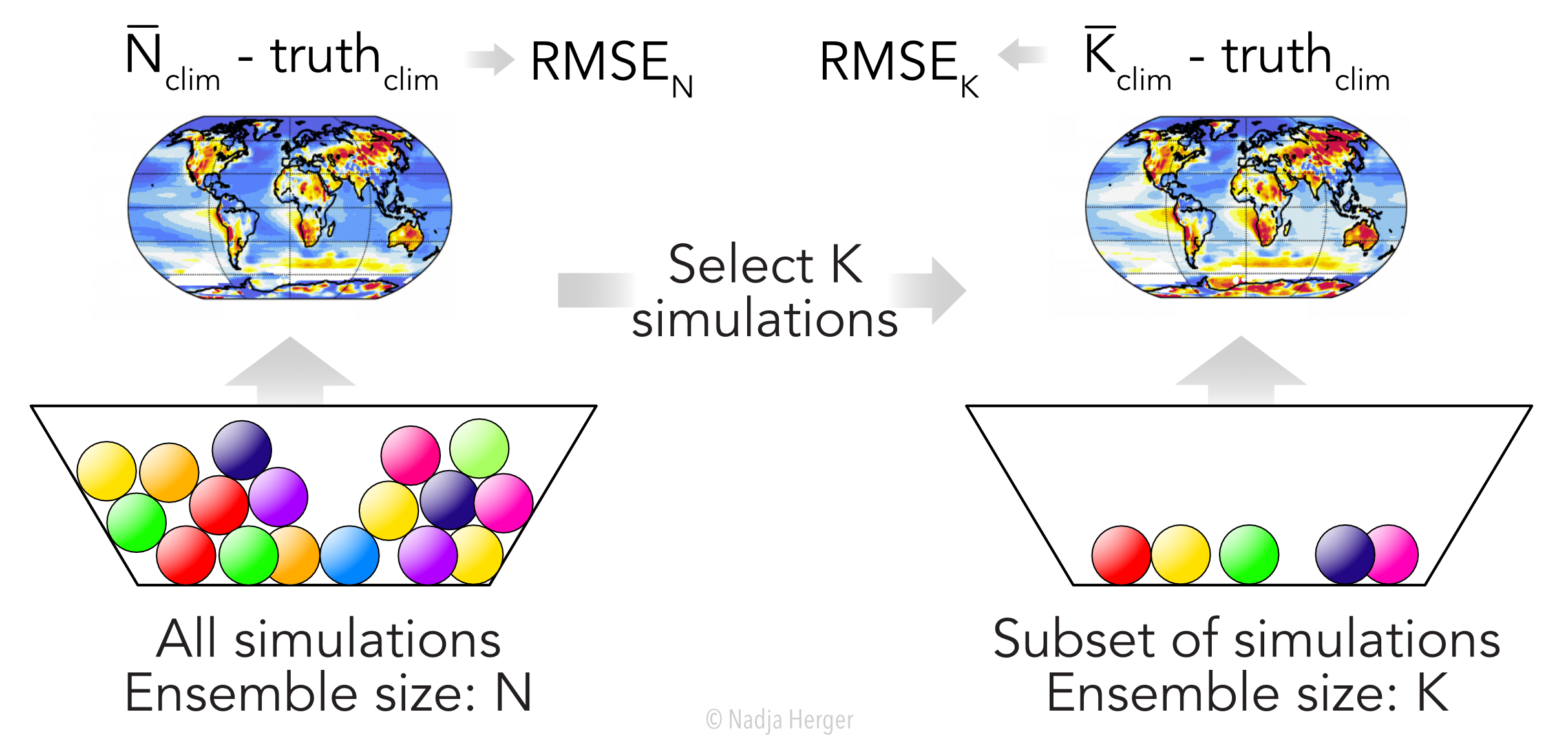
In the left basket we have N climate model simulations and after averaging the output of the N simulations, we can compute the RMSE compared to a given truth. We can then choose a smaller subset of simulations K (K<N) in the right basket and calculate the corresponding RMSE (between the mean of K simulations and the truth). For a given subset size K, the goal is to find the K simulations whose average results in the overall smallest RMSE. One possible way of tackling this problem is with brute-force, meaning that we can go through all possible combinations of K simulations, compute the corresponding RMSE and then choose the subset with the overall smallest RMSE. Unfortunately, this approach becomes quickly infeasable due to the long computing time. The computing time increases exponentially with the total number of possible combinations of simulations. With N=80 and K=40 for example, we would end up with 1.075072×1023 different combinations of simulations.
So, we need to find an alternative solution. This is where the state-of-the-art mathematical programming solver Gurobi comes into play. The problem itself is a mixed integer quadratic programming problem because the decisions are binary (a simulation is either part of the subset or it is not), the cost function is quadratic, and the constraint is linear. Gurobi makes use of the branch-and-cut algorithm to solve this problem. You can learn more about this algorithm and mixed integer programming here. Different to the brute-force approach, Gurobi’s computing time is insensitive to the total number of combinations. The subset that Gurobi finds is optimal with respect to the given cost function and boundary conditions.
Luckily, Gurobi is free for academic use and provides a Python interface. You can find a sample Python script to conduct subset selection using Gurobi in my GitHub repo.
If you want to learn more about this project, please check out my publication in Earth System Dynamics.
- Lessons learned in AI Governance
- My Journey from Climate Science into Responsible AI
- Photo Clustering
- Multi-objective optimisation and Pareto optimality
- Out-of-Sample Testing in Climate Science
- Climate Change Scarf
- Hackathon
- Combinatorial optimisation with Gurobi
- Visualising the model space with unsupervised learning
- Setting up Jekyll on GitHub Pages
